Mission Assurance
.png?width=400&height=400&name=No%20background%20%20-%2030%20years%20logo%20(1).png)
.png?width=500&height=333&name=Desktop%20Screenshot%20Test%20Version%20Only%20(delete).png)
SPEC Innovations provides innovative, cloud-native software solutions that encompass the full lifecycle of a system or product through requirements to MBSE to Human-Performance, all powered by AI.
Our training courses focus on the topics of DoDAF and Systems Engineering taught by experts in the field. We also have expansive training courses on our software, Innoslate and Sopatra. Courses can be taught in-person, on-site, or virtually.
Our team of experts have specialized capabilities in systems engineering, digital engineering, proposal development, and DoDAF. Our goal is to provide our clients with innovative services and solutions in a timely, professional, and cost-effective manner.
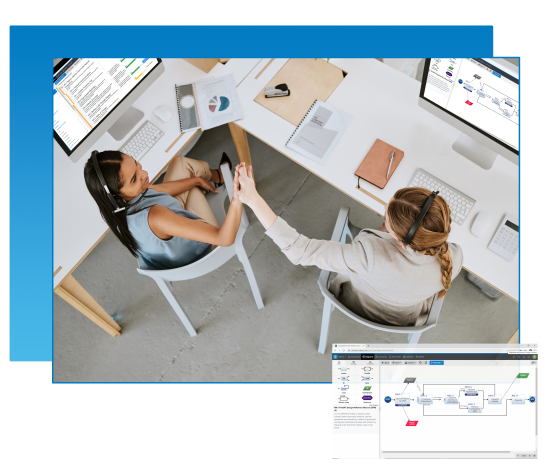
Innoslate is the first cloud-native, model-based systems engineering solution. Teams can work in real-time collaboration with version control in all areas of the product or system lifecycle.
Innoslate supports requirements management, modeling and simulation, verification and validation, program management, and more. See how Innoslate is the right solution for your team.
You do it all. You and your team cover the entire engineering lifecycle encompassing a myriad of fields and industries. It's about time you had a solution that can do it all too.
.png?width=64&height=64&name=target%20(3).png)
.png?width=64&height=64&name=evaluation%20(1).png)
.png?width=64&height=64&name=secure-shield%20(2).png)
.png?width=64&height=64&name=node%20(2).png)
.png?width=64&height=64&name=financial-report%20(7).png)
.png?width=64&height=64&name=chip%20(1).png)
.png?width=64&height=64&name=flow-chart%20(1).png)
.png?width=64&height=64&name=requirements%20(2).png)
We’ve curated over a hundred documents and models for you to use so you don’t have to start from scratch. Need JCIDS? We have it. Need MIL-STDs? We have it. Need Electrical Bonding for NASA? We have that too. Find what you need, import it into your project, and evolve the models and documents to fit your needs.
Discover the full library of digitally curated documents and models.
.png?width=128&height=128&name=help%20(2).png)
We provide our clients with innovative services and solutions in a timely, professional, and cost-effective manner. We serve commercial, defense, aerospace, intelligence community, federal civilian agencies, energy, and more.













Talk to an expert about implementing data-driven engineering into your organization.